There’s been a decades-long debate in the neuroscience community about how the brain processes information and forms memories. Two main theories exist: One states that the brain encodes information based on the rate at which there’s a spike in neurons—brief electrical impulses referred to as neural firing. So, higher neural firing, for instance, would mean there’s more communication between the neurons because more information is being processed. The other theory focuses on the precise timing of neural firing, suggesting that it’s not how much or how often they fire but rather when—and it’s those subsequent patterns of spikes and intervals between them that contribute toward information processing and memory formation.

To understand this, imagine cells in the brain serving as a kind of GPS; each time we pass a particular location in our environment, specific cells—related to that location—light up or spike. As this continues, cells continue to spike forming a path of sorts until we get to our destination. Researchers refer to these cells as place cells, and the spiking of these individual cells in relation to the environment are place fields.

While there’s increasing experimental evidence that points to the importance of these spike times and patterns across the brain, a mathematical approach to understand these patterns has been lacking until now.

Researchers with the NeuroNex Project, The Fabric of the Primate Neocortex and the Origin of Mental Representations, recently developed a mathematical technique to characterize patterns in spike times across many neurons. As a first example, they applied this technique to a phenomenon called “phase precession” in the hippocampus, which serves as a particularly clear case where precise spike times play a role in brain processes such as learning and memory formation. They published their findings in Physical Review E.

As part of the effort to decode these spikes, researchers looked at the pattern of neural firing in rodent brains as the animals navigated their surroundings.

Here, we see an illustration of neural activity in a rodent hippocampus. At the top, we see the rate of five neurons, N1-N5, spiking as the rodent navigates its surroundings along a straight path. The middle row provides an example of how the phase of each neural spike systematically advances in relation to the other neurons while, in the bottom row, we see a complex-valued representation of the pattern formed by the phase precession of neurons N1-N5. Illustration credit: Lyle Muller.

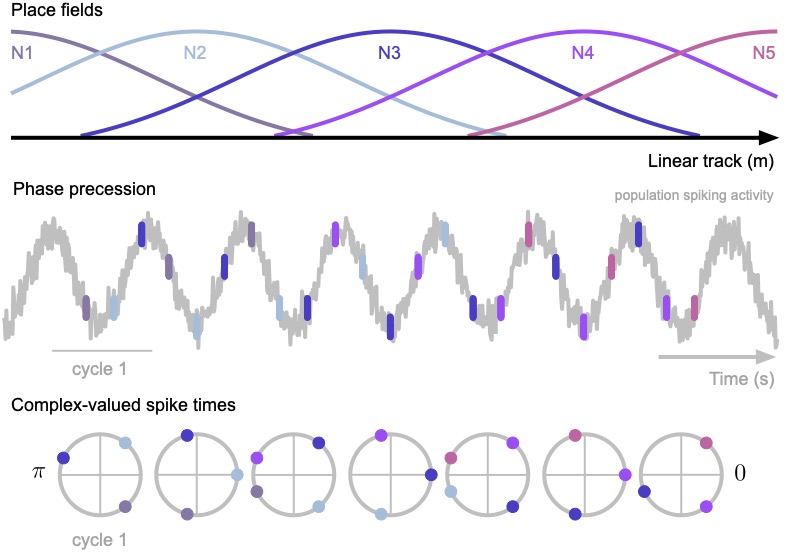
“What we wanted to know was how can we write that pattern as an equation that takes into account things that would be relevant for the brain while it’s doing it,” says Alexandra Busch, a researcher at Western University London in Ontario, Canada and co-first author of the paper. The equation they came up with focused on two things: the animal’s starting position and spike times. What they found as a result of their mathematical calculations was that the spikes weren’t just related to the animal’s current location but rather that the pattern of spike times created a link between where the rodent had been and where it was headed—essentially predicting future movements, all based on the way in which those spike times changed.

The hippocampus is well known as a brain structure important for long-term memory, and the phenomenon of phase precession has been directly linked to this process. “The hippocampus is often thought of as a ‘cognitive map,’ mapping out the environment like a GPS,” says Busch. “We believe these equations can help us make a link between the navigation and learning components of hippocampal function. Further, we also see a memory component, where we've got a little bit of the past, we've got a little bit of the future, and where we are right now, so that the system looks like more than just a GPS.

For Federico Pasini, assistant professor in the Department of Mathematics at Huron College in Ontario and co-first author of the recently published paper, a turning point was realizing the “precise relationship between events in the real world and patterns of spikes in the hippocampus, encoding memories of these events, could be reduced to geometric proportionality relationships. Once we found this link, we were able to use Thales’ intercept theorem, a 2,000-plus-year-old piece of knowledge, to write out precise equations for the spike pattern in this area.”

There are potential medical applications to this research as well, says Busch. For instance, researchers could use this understanding of neural patterns to analyze a breakdown in these kinds of patterns including the lack of memory formation, for instance in patients with neurological conditions such as Alzheimer’s.

“Having a mathematical language for these patterns can allow us to ask questions directly in recordings to understand how spike patterns change across health and disease.”